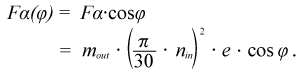5.8　カムとクランクシャフト
周期的な直線動作は機械的なドライブユニットであるカムとクランクシャフトを使用することで実現可能です。その代表例の一つは、ポンプのピストン動作です。動作の振幅が偏心距離eで与えられるとすると、ピストンの全ストークは2eとなります。

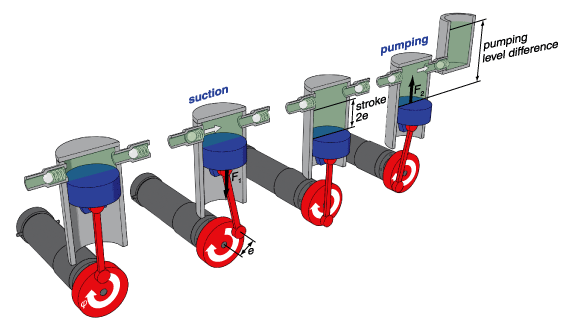
図 5.12: ピストンポンプ実例におけるカムドライブ

カムの計算
動作固有の短周期によって、カムの計算では、他の機械的ドライブの場合とは異なる別の検討が必要となります。負荷特性は、入力軸の各回転の後で反復されます。多くの場合、回転角φと負荷動作の両極点上の原点をパラメータとする動作周期とみなせば十分です。
一定のモータスピードn_inを想定する場合、これは毎分の動作周期n_out(n_in=n_out) から直接算出することができ、その結果はほぼ、負荷の正弦波速度カーブになります。

 

この速度特性で動作させるには、負荷とピストン、ロッド（質量m_outで統合）が恒久的に加速しなければなりません。これは、回転角の機能である周期的加速力が必要であることを意味します。

 

 

多くのカムで、後方動作と前方動作の間には異なる負荷条件が存在します。ポンプの場合、例えば、それぞれ異なる抵抗(管の直径と移動する長さ、摩擦条件、粘性)とリード厚(流体柱の高さ)に抗しながら、動作周期の最初の1/2の間に流体を吸引し、次の1/2の間に排出しなければなりません。周期の最初の1/2と次の1/2に、一定の力(F_out1とF_out2)に抗してカムが動作しなければならず、また加速力を考慮する場合、それぞれの角度において適用しなければならないトルクは、

  M_in1(φ) = e ・(F_out1 ・ sinφ + F_α1 ・cosφ) 　0 ≦ φ ≦ π
  M_in2(φ) = e・(F_out2 ・ sinφ + F_α2 ・cosφ) 　π ≦ φ ≦ 2π

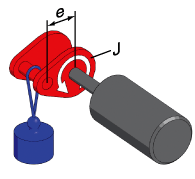
図 5.13: カムドライブのパラメータ
出力(負荷、out)は青で表示。
入力(モータ、in) はグレーで表示。

 

動作周期中の平均負荷トルクは、動作周期の1/2の2個分に対する実効値(rms)です。

 

この計算式では、容易に決定することのできる出力振幅だけが考慮されている点に留意する必要があります。効率はカムのベアリングシステムとピストンにおける損失を表します。
偏心カム(慣性モーメントJ )を、要求される周期周波数まで加速(持続時間Δtα)するには、追加トルクとして下記が必要です。

 

検証すべき追加要因
カムドライブのベアリングシステムには特に注意が必要です。ラジアル荷重もまた周期性があり、負荷として同じ振幅を持っています。ベアリングシステムは少なくともこの最大値に合わせて設計しなければなりません。特に、カムは摩耗やバランスずれが起こり得るため、高速回転するベアリング内でさらに反力が発生する可能性があります。